How-To: SIMD Programming
An introduction to practical SIMD programming and common pitfalls
If you’ve been programming for a while, especially at a low level, you have almost certainly heard of SIMD. Single instruction, multiple data (SIMD) is exactly what it sounds like — it allows you to process multiple pieces of data with a single instruction. I like SIMD because it can often lead to 4x, 8x or even 16x performance speed ups when used correctly.
This post is mostly aimed at beginner—intermediate developers who haven’t programmed with SIMD a lot, but this might still serve as a good refresher for experienced programmers. This should be a good introduction to SIMD but don’t expect to become an expert after just reading this post ;)
Please also note that in this post we will only focus on x86/x64 SIMD. Other architectures are not covered.
In this post we will:
Understand the Basics of SIMD
Figure out how to Query SIMD support on PC
Know the different ways we can program SIMD
Compare pros & cons of each approach
Convert an example to use SIMD — with benchmarks
The typical Naïve approach
Doing it the right way with the correct mental model
Cover some tips & tricks to common problems when using SIMD
Notes on Architecting systems to be optimizable with SIMD
What is SIMD?
SIMD is an actual piece of silicon in the CPU. Here is a Die shot of AMD’s “Zen 1” core1 with the SIMD units highlighted in red:
You might notice that the SIMD region has this sort of grid-like pattern. I’m not a hardware person so I don’t know for sure why it looks like that, but when we dive into how SIMD works — I think it makes sense why the hardware might look like this.
A simple SIMD example would be the ability to multiply pairs of 4 different 32-bit values with a single MULTIPLY instruction, instead of needing 4 individual MULTIPLY instructions. The time it takes to complete a SIMD MULTIPLY is usually the same as a regular MULTIPLY, which means in our example we can get a 4x speedup using SIMD.
We are not just restricted to multiplication, there are a plethora of SIMD instruction types available: from common arithmetic operations such as Integer/Float add, subtract and multiply, to bit manipulation such as left/right shift and bitwise or/and/xor. We can also perform comparisons (equal to, greater than, less than, etc.), and perform memory operations such as load/store/move.
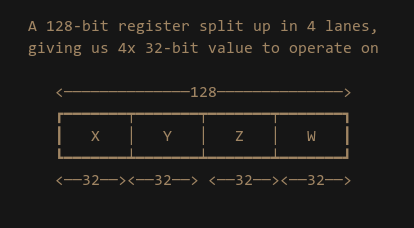
SIMD Registers & Lanes
When working with SIMD we use special registers which may be 128-bit, 256-bit or even 512-bit wide. These registers are then divided up in to “lanes”. Each lane contains one piece of data that the SIMD instruction will operate on. As an example: a 128-bit register with 4 lanes gives us 4x 32-bit values:
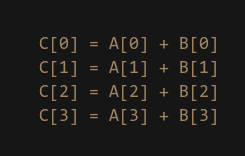
As I just mentioned SIMD carries out its operations on a lane by lane basis. This means if we issue a SIMD ADD instruction between two registers, it will perform the add for each lane “vertically”:
Another way to think about this is to image you are adding the values of 2x 4-element arrays together to produce a new 4-element array.
Understanding this concept is the most important part of SIMD programming. Working “across/horizontally” between lanes is not really something you do in SIMD. There are some cases where working horizontally is the correct operation, but in most cases I would argue you are probably doing something wrong if you need to go horizontal. This will make more sense later in the article when we look at benchmarks.
CPU Support for SIMD
How wide the registers can be and what kind of SIMD instructions are available depends on what the CPU supports. And here is where it gets a little bit complicated.
SIMD support comes in “Instruction set architecture” (ISA). The first SIMD ISA that was added to x86 was Intel’s Streaming SIMD Extension (SSE) in 1999. SSE supports 128-bit registers and has been upgraded over the years all the way up to SSE4. The “Advanced Vector Extensions” (AVX) ISA introduced 256-bit registers, and the AVX-512 ISA supports 512-bit registers.
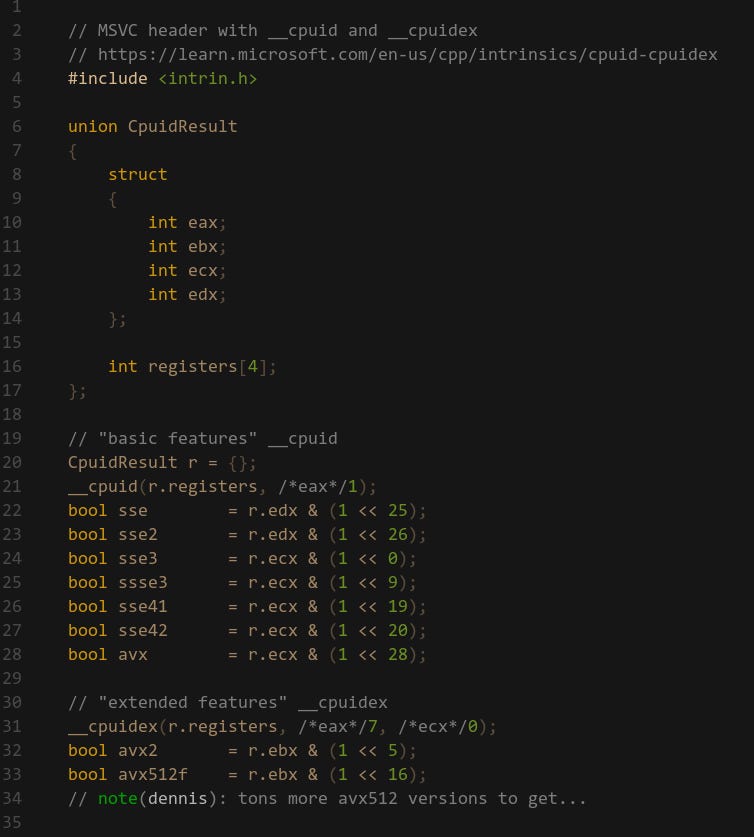
The support varies greatly depending on the hardware, you can query ISA support using the cpuid feature bits2. Here’s an example on Windows using the __cpuid and __cpuidex intrinsics3:
If you attempt to execute SIMD instructions on a machine that doesn’t have support for that instruction then your program will fault and crash. Thus, it’s important that you ensure the target hardware has support for whatever SIMD ISA you put in your program.
I would recommend picking a min-spec ISA that users require to run the program. As of April 2024, >99% of users on Steam has SSE4.2 support4 which makes it a very reasonable min-spec for games. Nearly 94% of users support the AVX2 ISA which makes it very tempting for us since the register size is double that of SSE — meaning up to double the performance. But leaving out 6% of potential customers is not insignificant, so I would not recommend using it as min-spec. A better approach would be to have SSE4.2 min-spec but only enable AVX2 for those which support it. This sounds simple but can be hard in practice. We will look more into managing this later.
Getting started with SIMD
There are a few different ways that you can program with SIMD. I’ll cover three different approaches and then finally go over pros—cons of each one.
Explicit SIMD with intrinsics
First, you can program SIMD explicitly by using whatever intrinsic functions that are exposed in your language. On Windows (MSVC) C/C++ the available functions and corresponding header files can be found on the Intel Intrinsics Guide5.
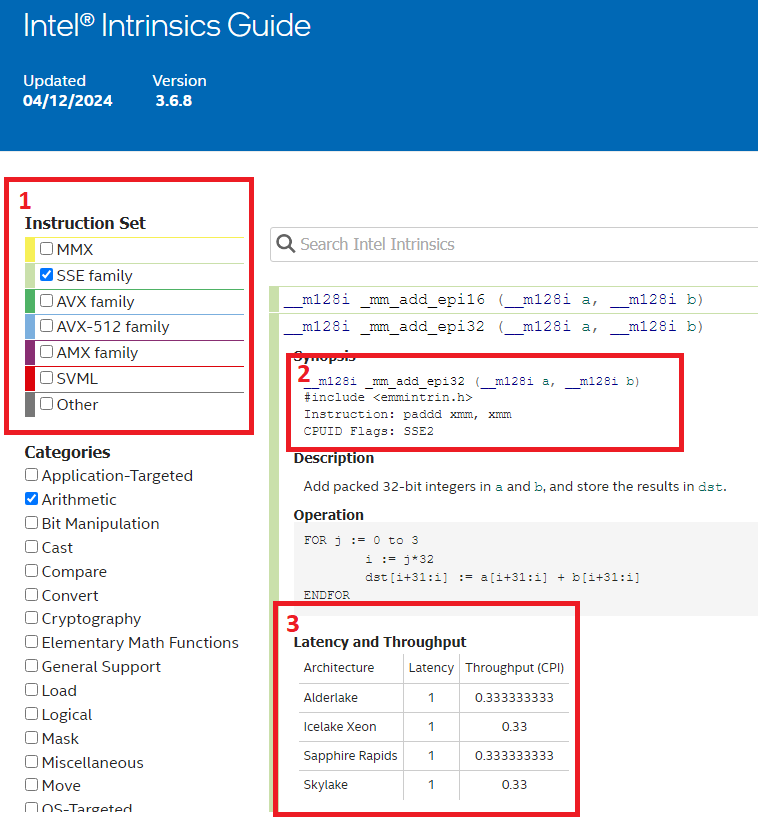
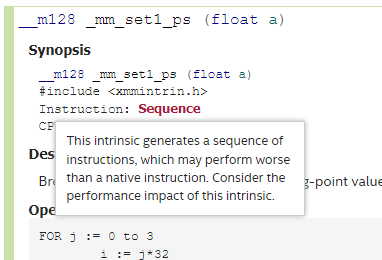
This is an awesome resource and is always on my second monitor when I program SIMD. It contains all available intrinsics for each ISA and detailed descriptions of them. Let’s take a look closer at the highlighted areas:
This filters the available intrinsics based on your target ISA. You can either pick “families” of ISA, or specific ones if you need.
Here we can see which header file the intrinsic is defined in, what x86/x64 instruction the compiler will generate and finally the
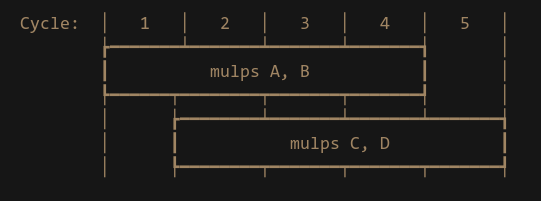
cpuidflag required.Performance metrics for Intel CPUs. This is very valuable to get a rough estimate of what kind of performance you can expect. You might already know what Latency & Throughput is, but just as a quick primer: Latency is how long it takes for the instruction to complete from the time it was issued. Latency of 4 clock cycles means it will take 4 cycles for it to complete. Throughput is how often we can issue the instruction. This is often measured in reciprocal throughput (although people usually don’t clarify if they are talking about reciprocal or not which can be confusing). A reciprocal throughput of 1 means we can issue the same instruction 1 cycle after the previous one, as long as the second doesn’t depend on the result of the first one. Reciprocal throughput of 0.33 means we can issue 3 of the same instruction on the same clock cycle. If we want to issue two float multiply instructions that have latency of 4 and throughput of 1, the total time for this to complete is 5 cycles provided they don’t depend on each other:
You’ll notice the mm prefix for the intrinsics. This stands for “multimedia” which is just a legacy term that we are still stuck with. But I digress, what you might notice is how verbose these intrinsics are, it’s almost like you are programming in Assembly. This is by design since the intrinsics are supposed to map 1:1 with whatever x86/x64 instruction it’s meant to generate. Sometimes, the Intel guide will say that an intrinsic is a “Sequence”, which means that it will generate multiple instructions.
It’s quite common to write a SIMD wrapper library that can make programming with SIMD a bit more enjoyable. But you need to be careful to not over-abstract your wrappers. When working with performance oriented code you want to keep abstractions to a minimum and eliminate uncertainties since all they do is get in your way and make it very hard to reason about your code.
Compiler Auto-Vectorization
The second option for SIMD, is to instead rely on the compiler to generate the SIMD instructions for us by “auto-vectorizing”. In reality though this should really be used in conjunction with explicit SIMD, as this is not a good option for reliably generating optimal SIMD code. Compilers are not magic — it’s just a tool that has to follow strict rules for what it can and can’t do. You have to play the compiler to have it generate the code you want. As a result, it’s very easy to one day have working auto-vectorized code, but then break it by just making a simple change to the code.
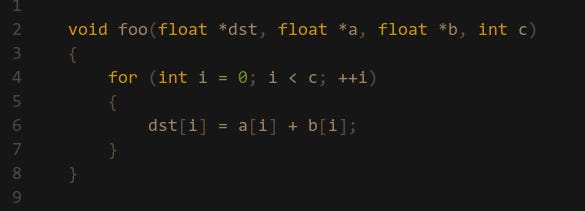
A very common restriction to compiler auto-vectorization is aliasing. Look at this very simple function:
You would expect the compiler to easily be able to generate SIMD code. But it turns out it can’t in a lot of cases. Because the pointer dst, a and b could all be the same, which means this code could break. A simple fix would be to add the __restrict keyword next to the pointers, which tells the compiler that the pointers are guaranteed to point to different places (but that doesn’t stop the programmer from still passing in the same pointer… ). However, the latest MSVC compilers will still auto-vectorize this, but it has insert additional checks to make sure the pointers are not aliasing.
There are plenty of restrictions to what can and can’t be vectorized, but at the end of the day the compiler must ensure the correct result over optimizations (unless you have undefined behavior). The key takeaway here is that you should always check the assembly output of your routine to make sure the compiler did the right thing, and I would personally never rely on auto-vectorization for parts of the program that are very important.
Auto-vectorization is usually enabled by default when compiling optimized builds. MSVC will try to vectorize your code when compiling with level /O2. I think this is also the case when compiling with Clang, but don’t quote me on this.
Intel’s ISPC compiler
The third option is to use Intel ISPC6. This is a custom compiler that accepts shader-like code (similar to that of GLSL or HLSL) and automatically compiles it to vectorized assembly code. You can then link these functions inside your C/C++ code like a normal function.
What I like about this is that you can write code in a serial fashion like you normally would. It also automatically picks the most optimal version to run based on what ISA is supported. When writing explicit SIMD with intrinsics we would have to maintain separate code paths depending on if we want to run the SSE, AVX or AVX-512 version, which adds complexity and maintenance costs.
I have not used ISPC too much so I can’t really comment more about it, but I like the idea of ISPC.
If you use Unreal Engine, ISPC is already integrated there and is used extensively in the engine.
Summary of Pros—Cons to each approach
Let's start with explicit SIMD. What I like about this is that it gives you full control over the generated code since the intrinsics often map directly to a single instruction. That way it makes it possible to make back-of-the-envelope calculations as to what kind of performance to expect. The control also allows you to make further optimizations by utilizing tricks, especially around floating point math that a compiler might not be allowed to do. Since you understand your program and the problem you are trying to solve better, you can write the best possible code yourself. However when working on large teams where the programmers have varying experience levels, SIMD code can be unintuitive, so only a select few might be able to maintain that code. Another disadvantage is when you want to support multiple ISAs. Supporting multiple ISAs means you need to write multiple versions of the same routine but at different widths (128, 256, 512, etc.). Unfortunately, this means that some applications only stick to supporting the min-spec ISA such as SSE and leave tons of performance on the table for users with AVX support (looking at you here Unreal Engine…).
I think the pros and cons of auto-vectorization are quite obvious. Not having to think about SIMD and just have the compiler magically take care of things is nice, and might lead to speed improvements in areas that you didn’t expect it. But as I’ve already mentioned you cannot rely on auto-vectorization for performance critical areas. You have to constantly check the assembly output to ensure the compiler did the right thing, because your code will silently break otherwise. Definitely let the compiler auto-vectorize code, but it needs to be combined with either explicit SIMD or ISPC.
When it comes to ISPC, as I’ve mentioned I don’t have tons of experience with it. But I can see the problems it’s trying to solve and I like what I see. The ability to just write code once and have it select the most optimal version based on the machines ISA support sounds very attractive. It would solve the two top complaints I have about explicit SIMD: better maintainability and support for multiple ISAs. Again, I haven’t used ISPC much but the only downside I can see is potential compiler bugs and it’s another layer of abstraction. More abstractions mean less control, which in turn may lead to worse performance.
Using SIMD
Alright, now that we know how to use SIMD let’s start coding. I’ll be writing SIMD using intrinsics since that’s what I’m most familiar with, and I recommend that you do the same as well when starting out. If you later choose to use an abstraction layer then the extra experience you’ve gained using intrinsics won’t hurt you.
The Naïve Vector Dot Product
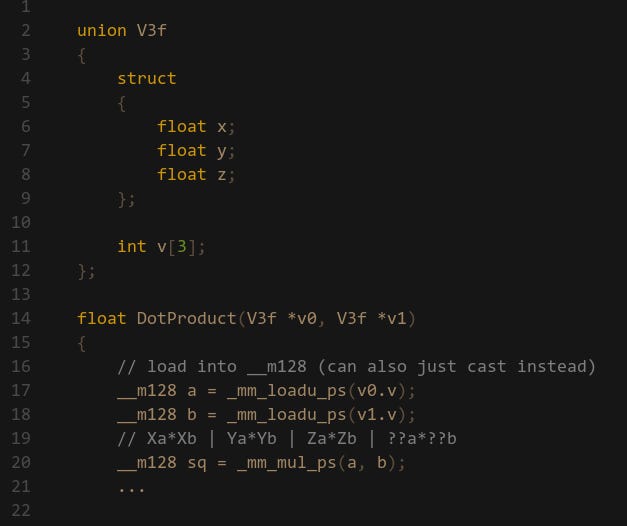
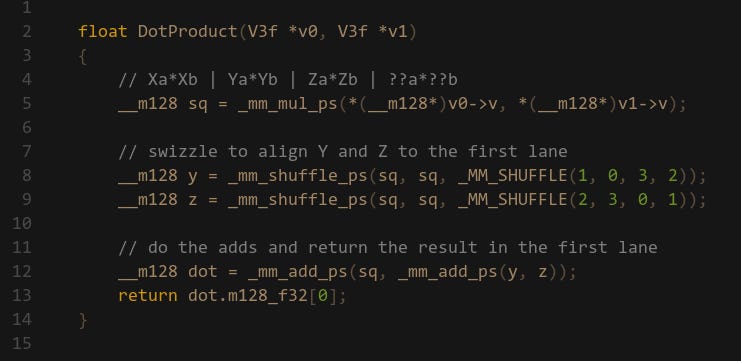
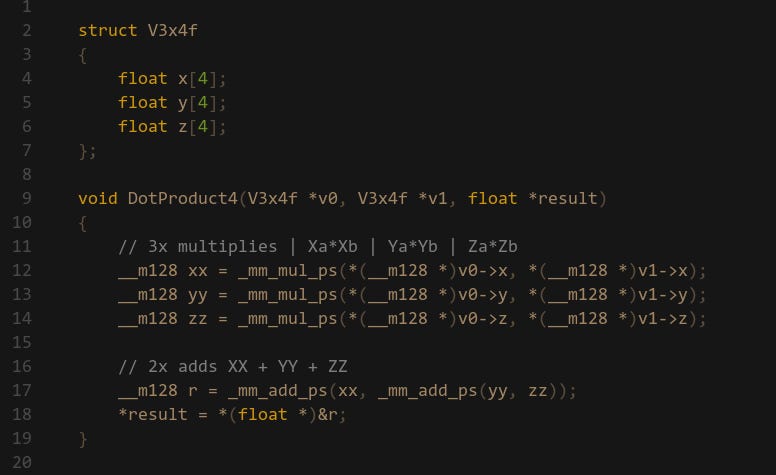
A very common first problem to convert to SIMD is a 32-bit float 3-vector dot product: Ax*Bx+Ay*By+Az*Bz it’s used everywhere (especially in games) and the operations are straight forward. We have 3x MULs and 2x ADDs. So we start with the multiplication and immediately run into a problem: the minimum lane width is 128-bit, but we only have 96-bits of data. One solution is to extend the vector struct by adding a 4th W component but this is a really large change which may have adverse affects on your codebase. Alternatively you can have a local variable that has the W component and copy the X,Y,Z components. The other option is to just include whatever data is at the end of the vector and treat the result as garbage. This is what I’m opting for here (spoiler: this can be a bad idea):
Alright now we’ve got the 3x MULs sorted, let’s do the additions. And this is where you run into the biggest problem: we have to operate horizontally for the adds. If you remember in the intro section, we ideally want to stay vertically with SIMD since that’s what it’s designed to do — there is not much support for working horizontally. Nevertheless, how do we solve this?
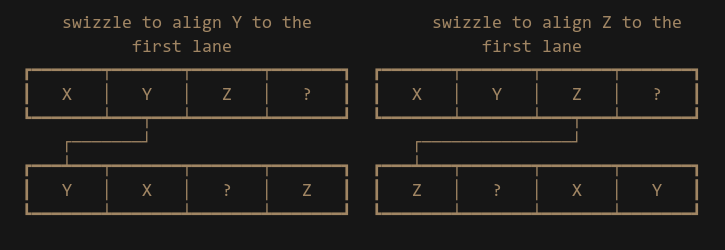
Let’s look at some solutions other people have come up with to this problem. Here is one answer from Stackoverflow suggesting to use Shuffles/Swizzles. If we dig into the Unreal Engine source code, we also find a VectorDot4 function that uses Swizzles, so this seems like the right approach, right? The idea is to have 3 copies of the multiplied result, then use swizzles to align the X, Y and Z components to the same lane:
Then we can go vertical again with the adds, and finally we will have the dot product result in that lane.
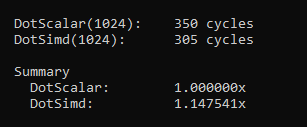
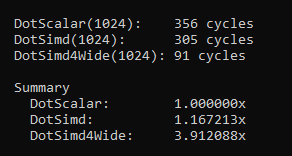
Alright great! I’m sure you’re excited to see some performance numbers. So let’s write a quick benchmark that runs our routine on 1024 pairs of random vectors. The vectors are laid out contiguous and memory access is linear in a tight loop. The cache has also been warmed up.
Alright, we get a little bit of speed gains compared to running a dot product function that isn’t using SIMD. But to be honest, this result is a bit disappointing. I’ve claimed multiple times in this post that we can expect 4x, 8x or even 16x speed improvements when using SIMD, so what’s wrong?
We are supposed to be processing multiple things at once — it’s in the name “Single Instruction Multiple Data”. But what we are essentially doing here is processing a single thing at once. Our mental model is “optimize this one single DotProduct”, when we should to be thinking “optimize multiple DotProducts“. We want to optimize for throughput — not latency. When using SIMD we have to change the way we think about our problems.
If we only have a single dot product to calculate then SIMD is probably not the right tool for this problem. But you almost certainly have multiple things that need to be processed, which is especially true in games. In our case we have 1024 dot products to calculate — so let’s process them in batches of 4 instead.
Vector Dot Product the Right Way
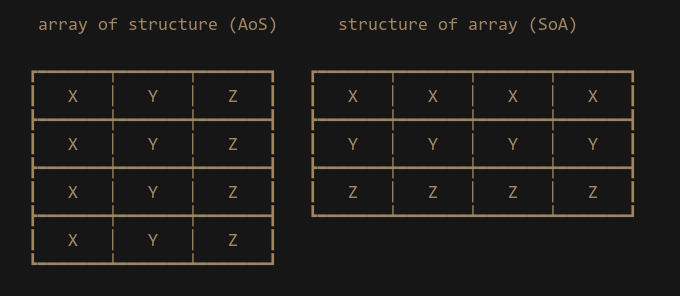
Now that we have rephrased our problem, let’s implement the correct solution. Starting with the input data, the dot products. Our data layout for the dot product has been a regular 3-wide vector. This is known as Array-of-Structure (AoS) data layout. But in order to process 4 different dot products, what we need is a Structure-of-Array (SoA) layout.
As you can see with the SoA layout the data is naturally organized into the correct lanes that we want. The X, Y and Z components are already vertically aligned so there is no need for us to swizzle the data — as a result the code becomes very straight forward:
When working with SoA data the routine naturally folds down in to SIMD. There is no trickery here, we have 3x MULs and 2x ADDs which is exactly how you would write a scalar dot product function without SIMD. Anyone can understand what this code does and how it works.
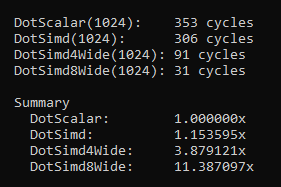
Now the moment of truth, here are the performance numbers:
Close to a 4x speedup using this approach. These are the kinds of results we should expect from using SIMD. Because remember, the latency & throughput of a scalar and the equivalent vector instruction is usually the same on modern hardware. Thus if we are not getting 4x, 8x or 16x speedups then this is typically a sign that something is wrong or we are not optimizing for maximum throughput.
I’ll also show a DotProduct8 routine that processes 8 individual dot products at once using AVX2, which is 256-bit wide.
I expected a 8x speedup but it turns out we exceeded that and are able to run at 11x! The key takeaway here is that this approach is scalable, whereas the previous approach isn’t.
Tips for SIMD
I’d like to share some tips and tricks that I like to use when working with SIMD.
Handling Branches
Control flow is usually a bit tricky with SIMD. Since we are working with multiple elements at once that means we can have N possible branches that need to be taken. If all elements have the same condition then there is no problem since they all take the same path and the program can continue as normal.
Using if statements in SIMD code is usually a code smell. An unpredictable/random branch will incur a 10-20 cycle stall (depends on your CPU) which can easily be more cycles than your entire SIMD routine. This is why it’s better to not have branches in the first place.
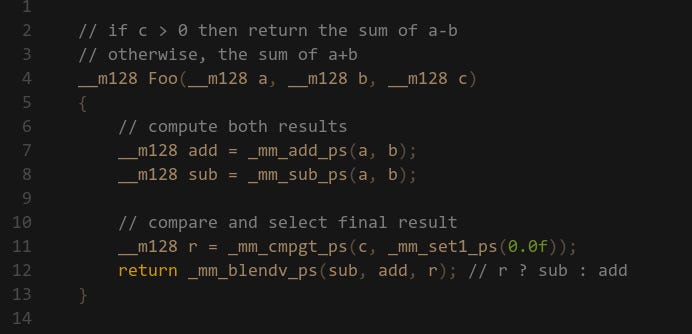
Sometimes you may go faster by doing more work, in our case that may be evaluating both sides of a branch then selecting the correct one, which is similar to what GPUs do. I like this approach because the performance is very predictable:
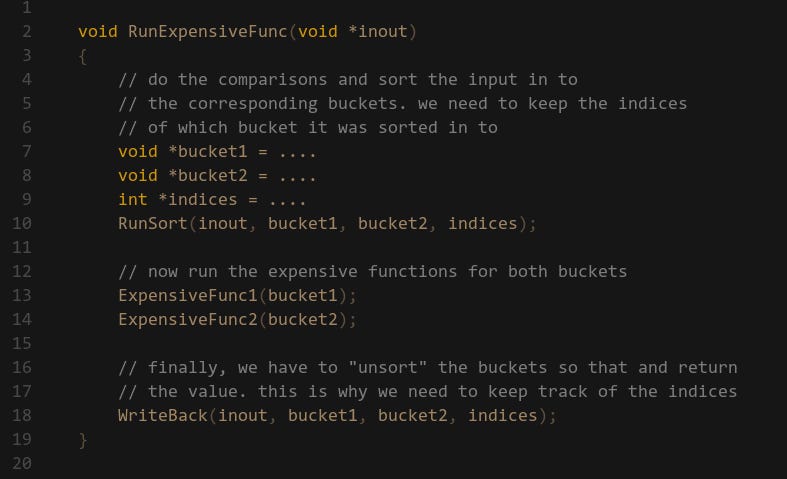
This might not always be a good approach — if the two sides require heavy computation then the select style can become too expensive. In cases like this I like to first sort the input data in to buckets, then run the if/else routines for the corresponding bucket.
In this case I have some input data which depending on a condition I want to either run ExpensiveFunc1 or ExpensiveFunc2. First I run a Sorting function that either copies the data from inout to bucket1 or bucket2 depending on the condition we are testing. We also maintain a list of indices which tells if we put the data in the first or second bucket. Then we are ready to run our main routines, one for each bucket. Once we are done we have to copy the data from the buckets back into the inout result. It basically just iterates over the indices we kept and copies either bucket1 or bucket2 into inout.
This means we have to maintain copies of the same data, but that’s okay. If we want speed we are happy to trade a bit of storage space. Another thing to note is that we could fold the WriteBack function into the main expensive function routines. Since the WriteBack is going to be memory move bound, we might be able to get that for free if ExpensiveFunc1/2 are heavy on compute. This highly depends on what exactly those functions are doing, so you need to experiment with the results. This is probably another topic that deserves a dedicated post….
I would also look in to “Parallel Prefix Sums” which can be very handy when doing this sort of stuff.
Uneven Input Data
It’s fairly common to have input data that are not at the correct stride for our SIMD routines, say we only have 15 elements but our routine requires 16 elements. We already looked at this in the DotProduct example, but one way to deal with this is to just ignore the last element by still performing the operation, but then discard the final value.
Though when doing this we have to make sure that the memory at the end is valid. It is possible that the data spans across multiple virtual page boundaries, and if one of those pages is not mapped to physical memory or if we don’t have permissions to write to that page then our program will fault.
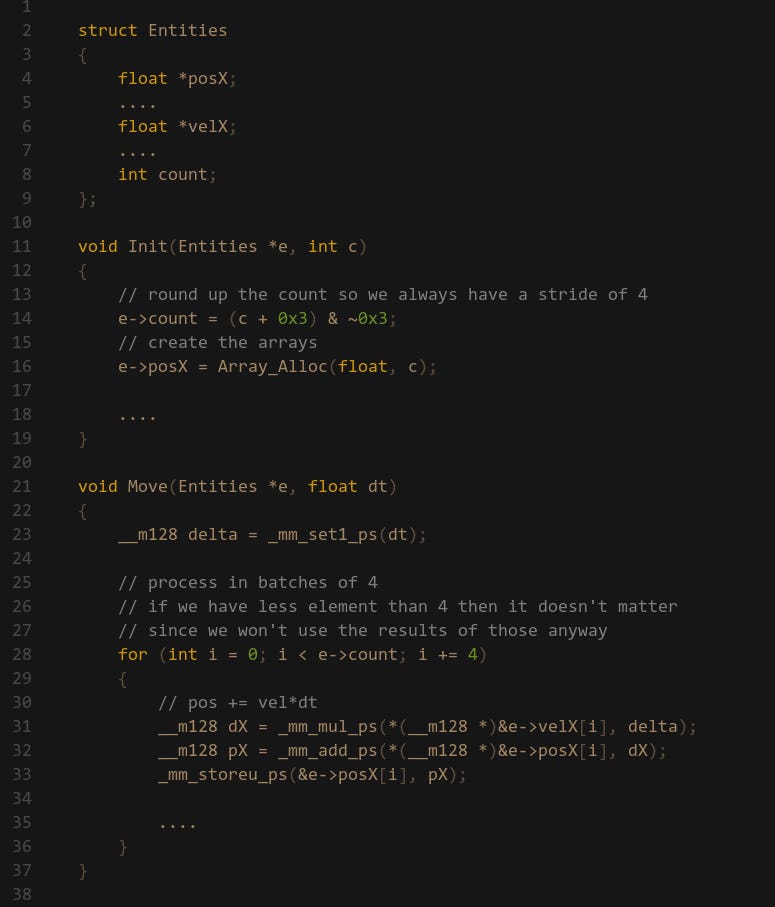
Alternatively, we can make sure that our input data is always padded so that it’s evenly aligned to whatever stride we are working with. If we are allocating arrays for some entities then I would round up the entity count and pad the end:
Now the Move routine doesn’t need to handle any special cases for when count is less than 4. The data at the end will just contain some garbage, but that’s okay since we will never use that data. At worst we are just wasting a couple of bytes of memory.
Use maximum stride when targeting different widths
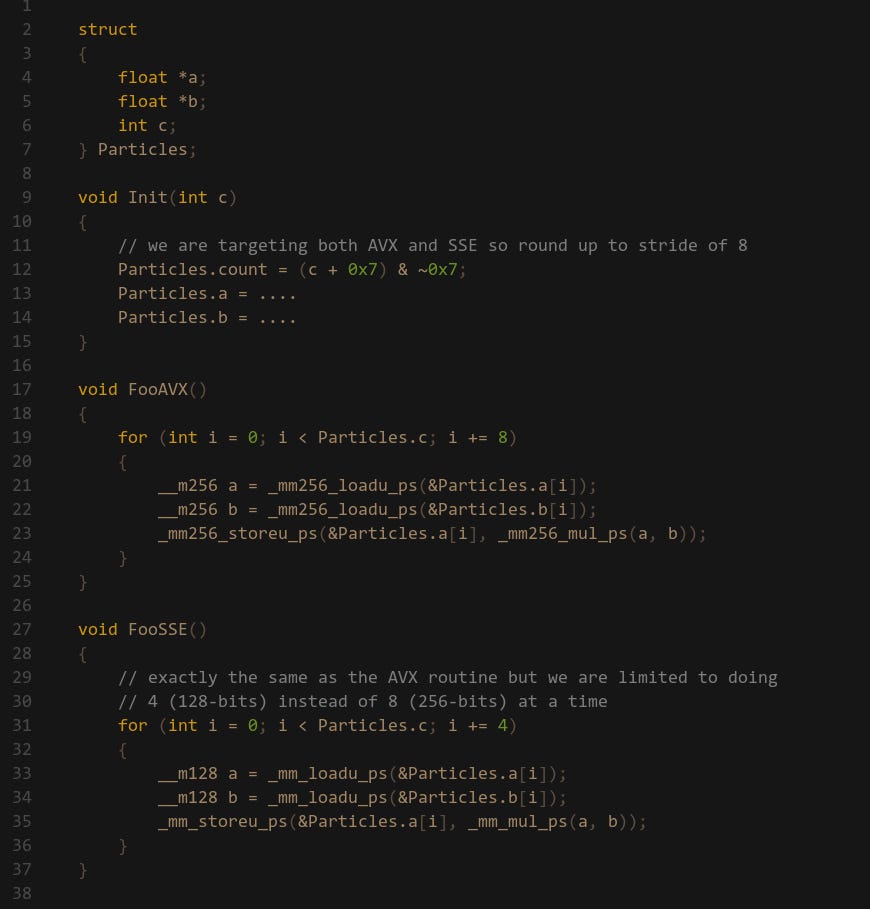
We need to properly handle targeting multiple ISAs, a common one is having 128-bit SSE as min-spec but also optionally supporting 256-bit AVX. In this case I would ensure that the input data is always aligned to a 256-bit stride since that is the larger of the two. We can then run a single AVX routine, but we will also be able to run SSE on that — we just have to run it twice instead:
So far I’ve found this to be the only reasonable way of handling multiple widths without ISPC. Obviously if we were to do the opposite and align to 128-bit stride while targeting AVX, then this wouldn’t work. This same principle can be applied to AVX-512, but then we’d instead have to align to 512-bit strides instead of 256-bit. I think it could make sense to implement some kind of abstraction here.
Quick note on Alignment
When moving data to and from SIMD registers, you have an option of using aligned or unaligned loads/sores, such as:
_mm_load_ps(...) // load 16-bytes at an aligned address
_mm_loadu_ps(...) // load 16-bytes at an unaligned addressIf you are going to use the aligned version, you obviously need to make sure that the address is aligned to a byte boundary equal to the register size (16-bytes for SSE, 32-bytes for AVX, etc.) If you don’t do this then your program will fault and crash.
In terms of performance, the aligned version is theoretically faster. Unaligned data may span multiple cache-lines — which means we have to load more cache-lines, and the load unit has to then merge from multiple load buffers.
However, in practice alignment is usually not a big problem. Because modern CPUs are heavily pipelined there is probably some other work the CPU can do while it deals with the unaligned penalty. It is a problem when you need maximum bandwidth and you aren’t doing much computation.
For this reason I typically use the unaligned load versions of the intrinsics and I rarely notice the performance penalty.
Writing ‘Optimizable’ code
In my opinion writing the actual SIMD code is not the difficult part of SIMD programming, where people often get stuck is typically at the data layout stage. If the data in our program is not structured correctly then there is not much we can do.
This is why it’s very important to keep SIMD and optimization in mind early on when designing a system. I don’t recommend to immediately start writing SIMD or optimizing code when first starting to implement a system, since that’s probably a waste of time. But you need to look ahead and see how you might be able to optimize the system in the future. If you don’t do this then you run a very real risk of not being able to SIMDize your code at all, since by the time you eventually start thinking about SIMD the system might be too complex, which might require a large refactor or even a rewrite of the entire system. As a result, the optimization might never happen.
Thinking about your data layout might also open the opportunity for other optimizations, such as multithreading and ensuring that caching behavior is ideal. To be honest with you, writing SIMD is usually the last step of my optimization process. Ensuring that your algorithm has the correct time-complexity and that the data is laid out in a way that’s ideal for the CPU cache then most code will run fast enough for you to not care. If I need it to run faster then the next step is to optionally move to Multithreading or SIMD, but again, the prerequisite is that we have architected the code in a way that allows us to do that.
Death by a thousand cuts is a very real thing, and the idea that you can optimize a program by fixing a few “hotspots” is a fallacy7. I can’t stress enough how important it is to just keep performance in mind early on.
Final Notes
Alright, I think I’ve about covered everything I want to. This is my first article so any feedback or comments would be appreciated.
I plan on doing in more of these, next on my list is probably talking about CPU caches or some of my Unreal Engine experiments.
But let me know what you’d like to see next!
~ Dennis





Hey man thanks for your article, it helped me when I was diving into simd. And it is a miracle that it showed up among dozens of AI articles.